Linked Lists - An Explaination and Implementation in C
One big topic we hit on in my data structures class is linked lists. To me, this was such an abstract concept and one I felt as if I didn’t have a good grasp on initially. After visiting my professor’s office hours to get a better understanding of this (which he did a great job at explaining it, for the record!), I took it upon myself to really have a deep understanding of not only what these are, but to implement them in a given language and then turn around and explain it to others who were in my position with not understanding of what they were.
This post will discuss:
-
What linked lists are.
-
A comparison in time complexities of Linked Lists and Arrays.
-
Sample implementation in C.
-
Demonstrating my implementation that can be easily integrated into your project.
The combined code used in this blog post (seperate from my personal implementation) can be found at the very bottom.
Section 1: What are linked lists?
Linked lists provide a way to dynamically store your data. Unlike arrays, we don’t need to know the size of the linked list in order to allocate the memory properly - it’s done on the spot.
Take a simple situation: appending a value (that is, add a value at the end of the array/linked list). In order to append a value with an array, you have to first create an empty array of the current size +1, copy the contents of that array, then add in the element at the end of the array:

With linked lists, you create a new “node” and reroute a pointer (or pointers for doubly linked list):
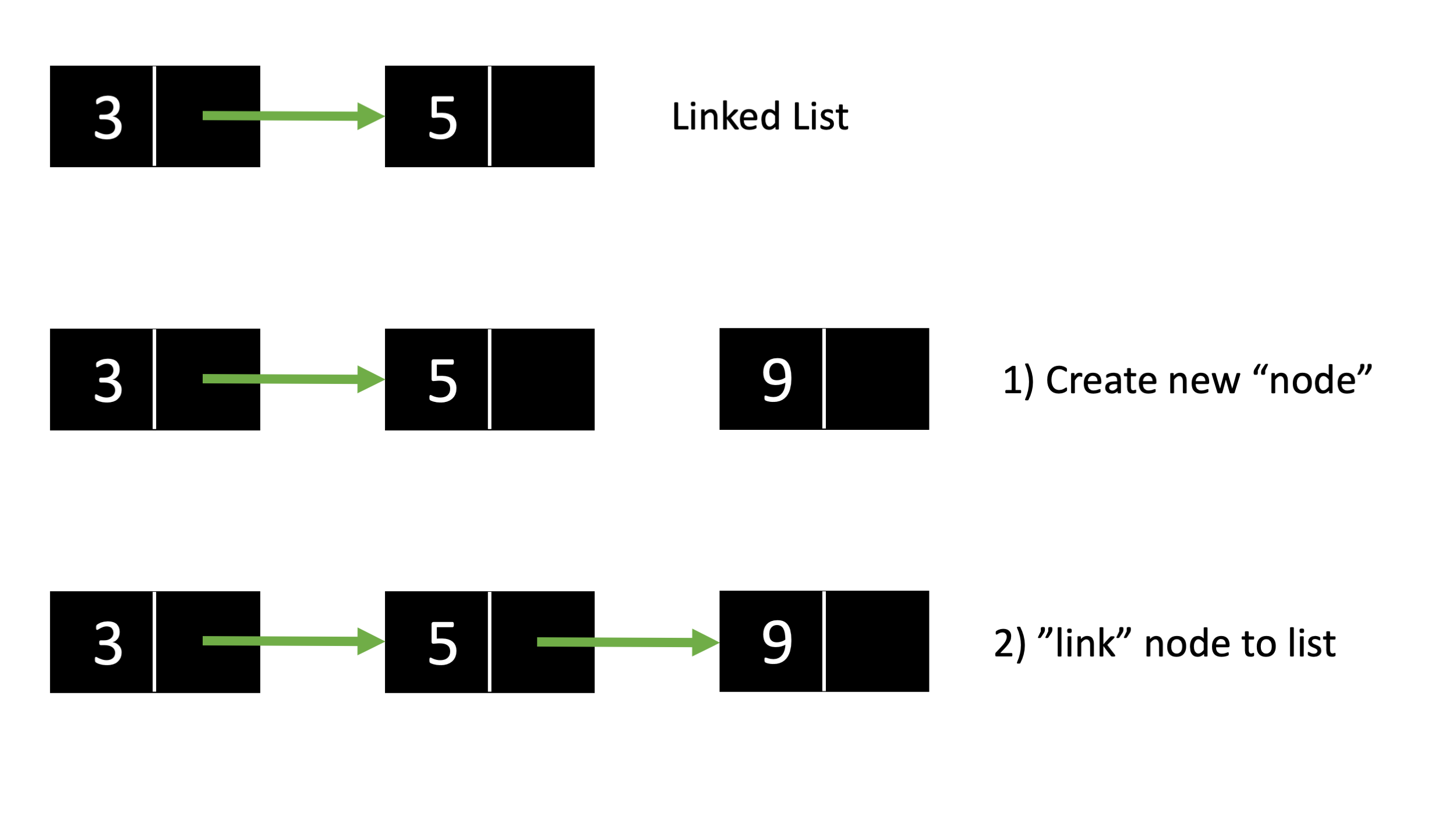
In the most basic implementations, a node contains 2 attributes: a value and a pointer pointing to the next node (which is typically initialized to null). More complex nodes can, for example, contain a secondary pointer pointing backwards to the previous node (hence, doubly linked list).
The primary advantage of using a linked list instead of an array is that you do not have to know the size of the linked list to allocate memory appropriately. In addition, adding an element to an array that’s full is a costly operation in terms of memory
Section 2: Time Complexity Comparison
The following table shows the worst case time complexities for both arrays and linked lists. Note the following assumptions:
-
It is an unordered list.
-
The
addoperation has a reference to the node that it wants to remove. -
The
removeoperation has a reference to the node that it wants to remove.
| Operation | Array | Linked List |
|---|---|---|
| Add | O(n) | O(1) |
| Remove | O(n) | O(1) |
| Search, index unknown | O(n) | O(n) |
| Search, index known | O(1) | O(n) |
It should be noted that average case also has the same time complexities, but uses $\theta$ instead of O.
Confusion may arise with why the remove operation is O(1) and not O(n). This is because of assumption #3 listed above - there exists a reference to the node that is to be removed. If there is no reference to the node, then you have to search the list, which is O(n). Once the search happens and the node is identified, then the steps to remove the node are of constant time (that is, O(1)).
Section 3: Sample Code in C
For the sake of illustration purposes, the following assumptions are going to be made to demonstrate an implementation in C:
-
The linked list is unordered.
-
Any
addoperations will be appended to the end of the list. -
There is a pointer pointing towards the front node and the rear node of the linked list.
-
The linked list elements are of data type
int.
Note that this is my personal implementation of linked lists. There are many other ways of doing this and you should go about implementing them in a way that makes the most sense to you.
High-level intuition
Before diving into the code, it’s always a good idea to think about what is needed.
-
Nodes (suggested: struct).
-
A reference to start the node chain (suggested: struct or pointer).
-
Methods:
-
add() -
remove() -
search() -
init_node() -
init_list()
-
The code
Data Structures
The first point made above is having a struct for nodes. This can easily be represented as such in a header file:
typedef unsigned int u_int;
typedef struct node {
int ele; // the value in the node
struct node * next; // pointer to next node
} int_list_element;
This takes care of individual nodes that are inside of the linked list. There’s also a decleration for an unsigned integer (u_int), as this is something that my personal implementation utilizes.
From here, we want a way to be able to reference the first node. You can either create a pointer to the first node or create another struct to point to the first node. It’s my recommendation that the latter is followed, as you can add various members to it (such as the length, sum, etc):
typedef struct {
int_list_element * front;
int_list_element * rear;
u_int size;
} int_linked_list;
Notice the data types of the pointers - they’re int_list_element. This is the node itself, so it should be noted that if you change the name of the node struct, you have to change the two pointer data types.
Now that the data structures of both the node and the list is in place, there needs to be a way to initialize these.
Initialization Methods: linked list, node, “current” node
The first thing that should happen before any node gets initialized is the creation of the list. The easiest way to do this is to create a pointer pointing to the list, allocate it in memory (so we can clear it later if need be), setting the members appropriately, and returning the pointer to the list:
// Initialize an empty linked list.
int_linked_list * init_linked_list() {
int_linked_list * list;
list = malloc(sizeof(int_linked_list));
list -> size = 0;
list -> front = NULL;
list -> rear = NULL;
return list;
}
Likewise with nodes:
// instatiates a new node to be added into the linked list.
int_list_element * init_new_node(int element) {
int_list_element * node;
node = malloc(sizeof(int_list_element));
node -> ele = element;
node -> next = NULL;
return node;
}
Although not required for this implementation, I like to have a supportive initialization function that allows me to insantiate a pointer to allow me to iterate through the linked list:
// initiates a pointer to iterate through a given list.
int_list_element * init_search_ptr(int_linked_list * list) {
int_list_element * current;
current = malloc(sizeof(int_list_element));
current = list -> front;
return current;
}
From here on, I will be calling this function to create a “current” pointer in the add, remove, and search functions.
Operative functions: add, remove, search
I’m going to be starting with the search function, as add and remove have to have additional considerations and assumptions.
The search function is a simple traversal through the linked list with a comparison with the given element as the traversal happens:
// returns 1 if element is found, returns 0 otherwise
u_int search_list(int element, int_linked_list * list) {
// create pointer to search through list
int_list_element * current = init_search_ptr(list);
while (current -> next != NULL) {
if (current -> ele == element) {
// element has been found
return 1;
}
current = current -> next;
}
// element has not been found
return 0;
}
The search function implemented above does not consider an ordered list. If it is an ordered list and you want your search function to incorperate this, then you can add in another comparison to check to see if the list element is greater than the given element. That is, the while statement would be:while (current -> next != NULL && current -> ele < element). If it is, then return 0, as all elements following the current node will be higher than the given element - there’s no need to search the list.
Both add and remove have to have special considerations. For example, is it an ordered list? Does it have to be in ascending order? Is it a doubly linked list? Do we have to have a way to insert into the middle of the linked list?
That being said, the add function should be implemented first, as the remove function requires even more considerations.
The intuition to append a node into a list is fairly straight forward: identify where you want to insert it, redirect “current” pointer to the new node, update rear pointer. Remember that the assumption made above is that all new elements are getting appended to the end of the list:
// Add in a node to the linked list.
u_int add_node(int element, int_linked_list * list) {
// initialize a new node and a "search ptr"
int_list_element * node = init_new_node(element);
int_list_element * current = init_search_ptr(list);
//Add node in the front
if (list -> size == 0) {
list -> front = node;
list -> rear = node;
}
else {
// list -> rear -> next is null; now the current node.
list -> rear -> next = node;
// update list rear pointer to node.
list -> rear = node;
}
// increment the size of the list.
list -> size += 1;
return 0;
}
Note that if you want to insert a node in the middle, it will require a few extra steps but the same intuiotion holds: identify location, point new node next member to next node, redirect “current” pointer to new node. Do not redirect the “current” pointer next member to the new node first, then point the next member of the new node to the linked list, as you will lose reference to the linked list. The code for this is not shown here.
All that’s left is the remove function. I had mentioned this requires a bit of extra thought, as there are many ways to go about it. Should only the first instance of the element be removed? What about the first n instances? How about all of them? And so on…
Here, I’m going to show how to remove the first instance of the element of interest (that is, remove the first element that appears):
// removes the first instance of the element in an unordered list.
u_int remove_node(int element, int_linked_list * list) {
int_list_element * current = init_search_ptr(list); // create new search pointer
// check to see if it's the first element.
if (list -> front -> ele == element) {
list -> front = list -> front -> next; // move front to next; current is still old front
free(current);
return 0;
}
// check to see if it's the rear element.
if (list -> rear -> ele == element) {
while (current -> next -> next != NULL) {
current = current -> next;
}
list -> rear = current; // set rear one back
current = current -> next; // move current to next node
list -> rear -> next = NULL; // set rear's next to be null
free(current); // free the current pointer; also frees the node
return 0;
}
// if it's in the middle
while (current -> next -> next != NULL) {
if (list -> ordered == true) {
if (current -> next -> ele > element) {
return 1;
}
}
if (current -> next -> ele == element) {
int_list_element * temp = init_search_ptr(list); // create new search pointer
temp = current -> next; // temporary pointer to the node to be removed
current -> next = current -> next -> next; // "hop" pointer over node to be removed
temp -> next = NULL; // set the node to be removed
free(temp); // remove it entirely.
return 0;
}
current = current -> next;
}
return 1;
}
Here’s an illustration of what’s going on in all 3 remove scenarios:
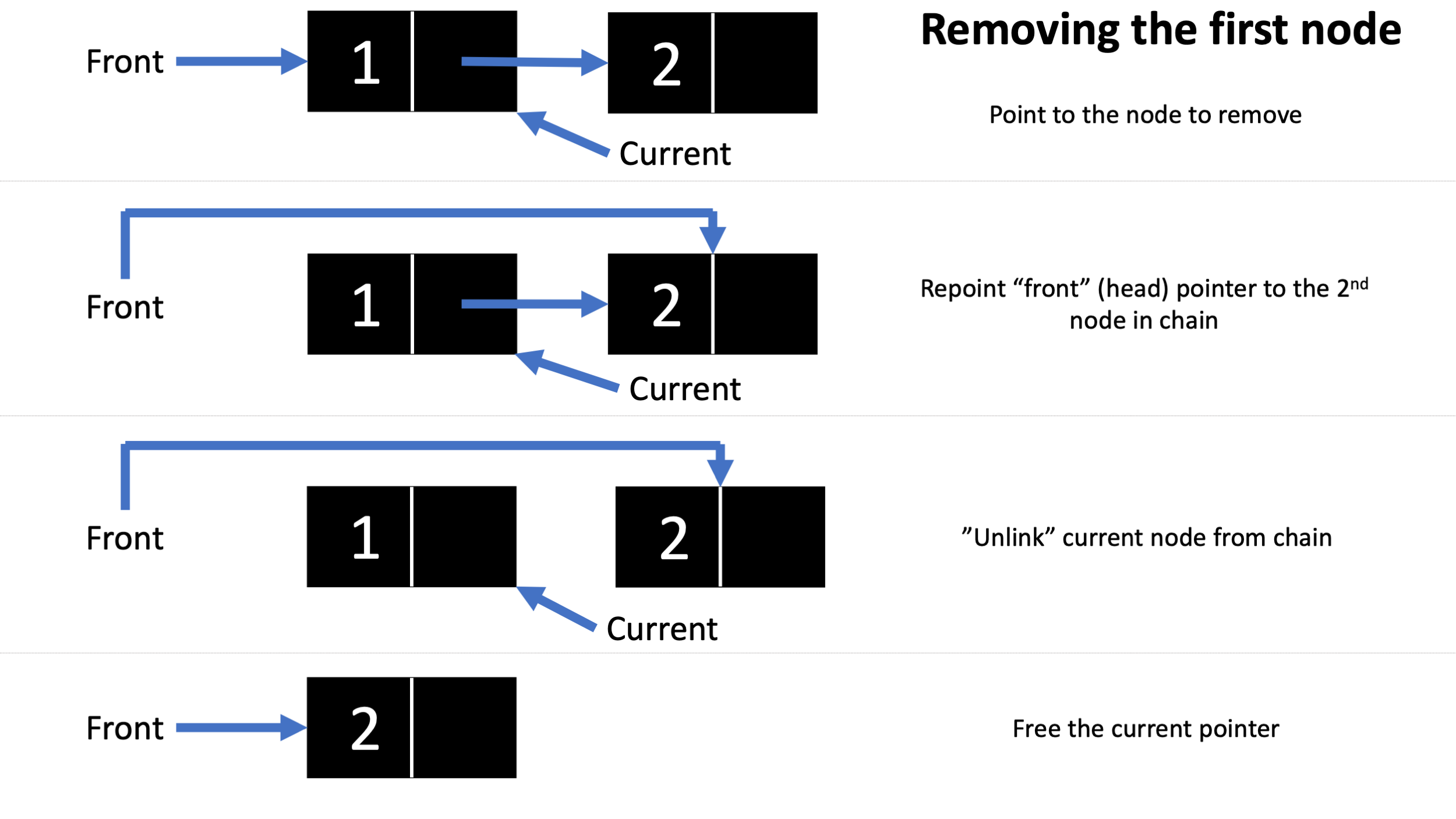
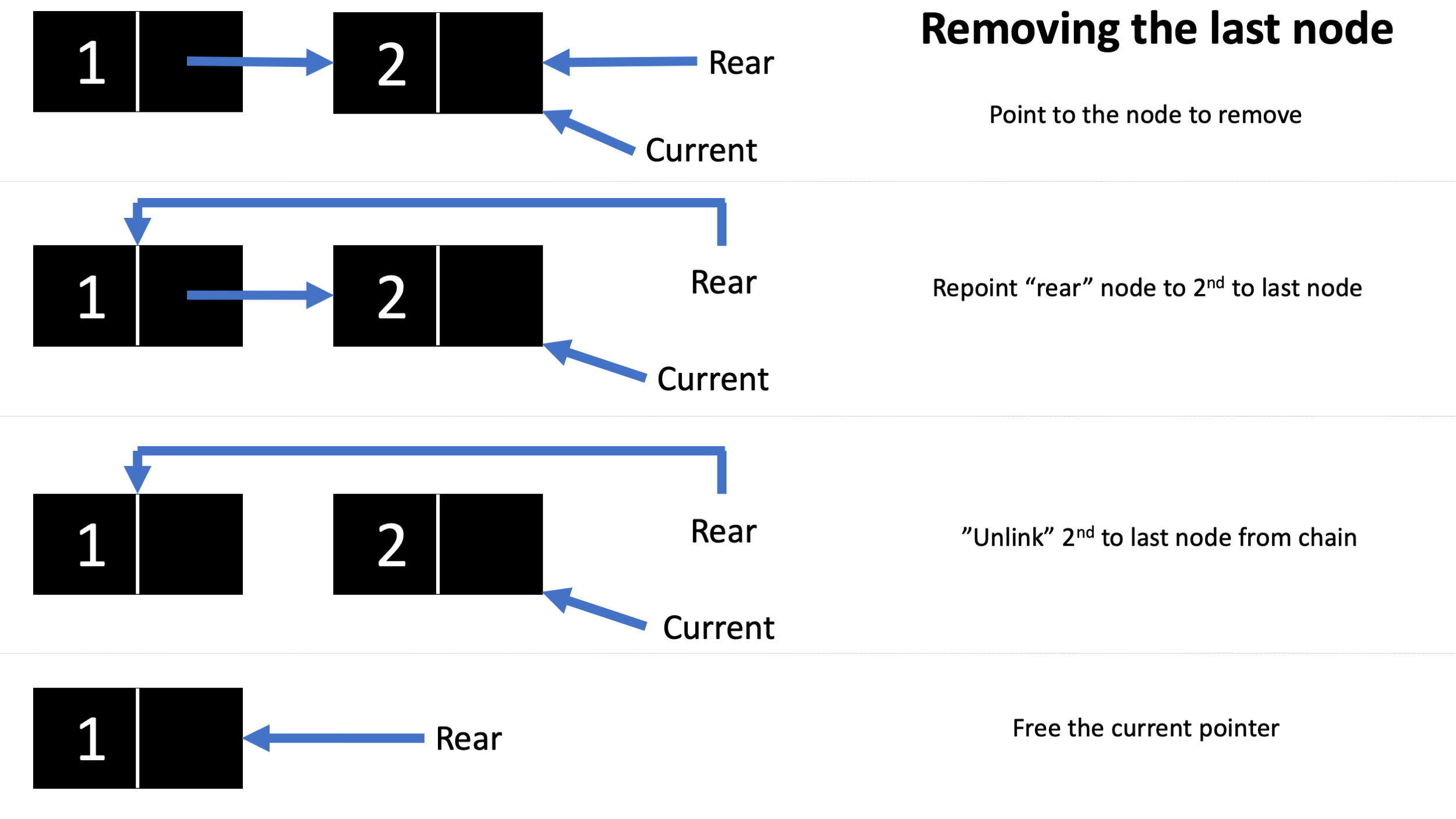
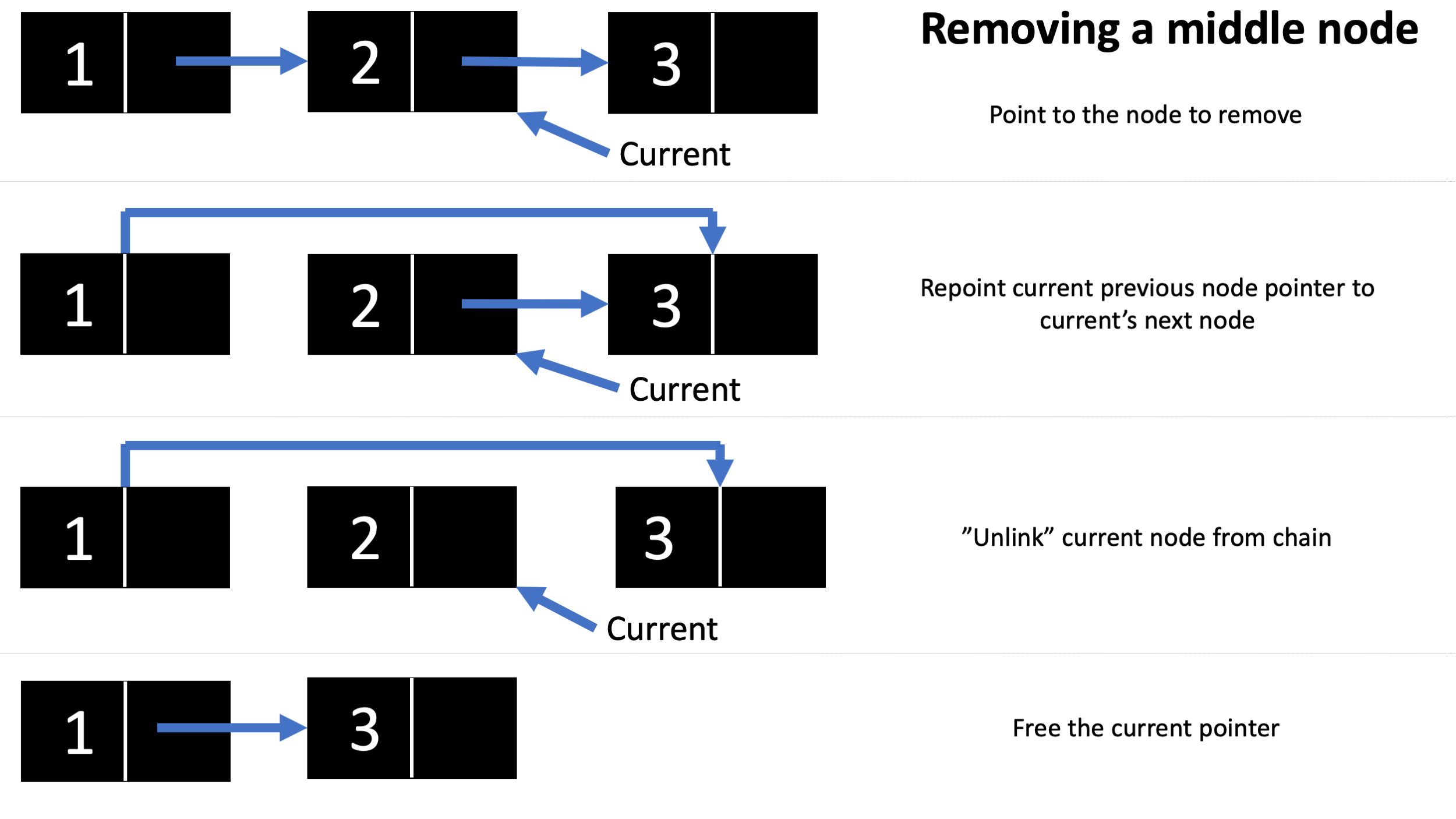
However, it should be noted that in the implementation above, we keep the current pointer to the node we want to remove previous. That is, if we wanted to remove the node with element 2 in the above diagram, the “current” pointer will be pointing towards 1 instead, as there is no way to go backwards once you traverse forwards.
Section 4: My Implementation With Integration Into Your Project
I have spent some time to make this integratable into your project with relative ease. The source code and explaination on how to go about doing this can be found on GitHub.
In this mini-project, I included different kinds of linked lists: ordered and unordered, as well as allowing and not allowing duplicates. For ordered lists, you can also declare if it’s going to be in ascending or descending order.
For example, if you wanted to instantiate an unordered linked list and add an element:
int main {
int_linked_list * list = init_unordered_linked_list();
add_element(6, list);
}
More can be found in the README file in the repository.
If this post has helped you at all, I’d love to hear about it! Tweet at me [@WxBDM](https://twitter.com/WxBDM or shoot me an email.
